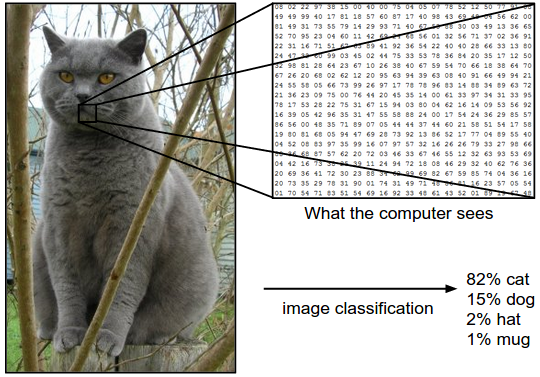
다음과 같은 고양이를 분류할 때 어려운점은 무엇일까요?
- viewpoint variation : 물체가 항상 똑바로 서있지 않습니다. 다양한 각도로 회전이 되어 있을 수 있습니다.
- scale variation : 영상안에서 다양한 크기로 있을 수 있습니다.
- deformation : 사람또는 동물이 다양한 자세로 있을 수 있습니다.
- occlusion : 물체의 일부만 보일 수 있습니다.
- illumination conditions : 영상의 밝기에 따른 픽셀값이 천차만별입니다.
- background clutter : 배경과 아주 유사한 모양의 물체일 수 있습니다.
- intra-class variation : 같은 고양이어도 다양한 종이 있습니다. 종에 따라 특징이 다릅니다.
영상 클래스를 분류하기 위해서는 위의 어려운 점들을 해결해야 합니다.
Nearest Neighbor Classifier
가장 기본적으로 생각할 수 있는 알고리즘입니다.
이 알고리즘은 기준이 되는 영상과 분류할 영상의 픽셀차이로 분류하게 됩니다.
픽셀차이를 계산하는데 기본적으로 L1 distance를 생각할 수 있습니다.
\[d_1 (I_1, I_2) = \sum_{p} \left| I^p_1 - I^p_2 \right|\]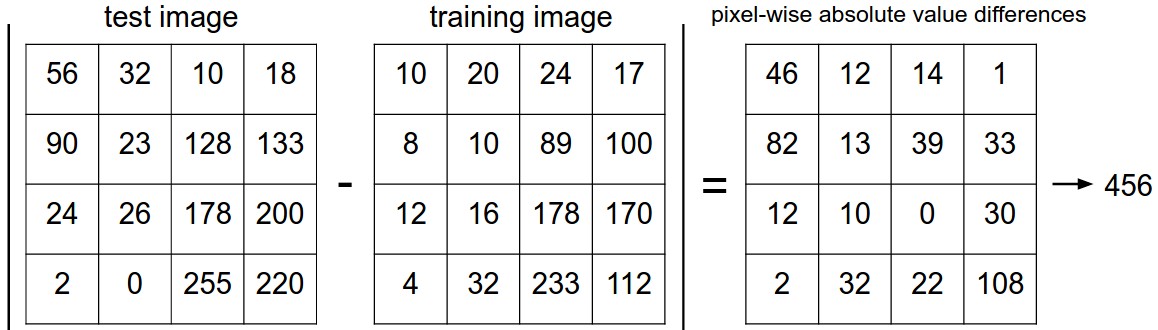
학습영상과 분류할 영상의 L1 distance를 적용한 그림입니다. 차이가 456인데, 일정 임계값을 정하고 “임계값보다 작으면 고양이다” 이런식으로 분류를 하게 됩니다.
L1 distance과 다른 방식인 L2(euclidean) distance는 다음과 같습니다.
\[d_2 (I_1, I_2) = \sqrt{\sum_{p} \left( I^p_1 - I^p_2 \right)^2}\]좌표계로 생각했을 때, L2 distance는 특정 좌표점을 기준으로 원으로 그린 거리입니다.
이 메커니즘을 이용한 regularization 방법은 딥러닝 학습에 유용하게 쓰이므로 알아두는 것이 중요합니다.
자세한 내용은 추후에 따로 포스트하겠습니다.
k-Nearest Neighbor Classifier
이 알고리즘은 어떠한 데이터를 분류할 때, 데이터와 가장 가까운 k개의 데이터를 보고 분류하는 방법입니다.
k=1이면 데이터와 가장 가까운 한개의 데이터만 보고 분류하는것입니다.

위처럼 데이터가 있을 때, NN classifier와 5-NN classifier를 사용하여 분류한 범위를 보여줍니다.
k=5일때가 k=1일때보다 군집이 더 잘된 것을 볼 수 있습니다.
k=1인 경우, 이상데이터에 의해서 군집이 잘 안되었습니다.
그런데, 가장 이상적인 k값을 어떻게 구할까요?
Validation sets for Hyperparameter tuning
가장 이상적인 k값을 구하는 일 뿐만 아니라, 다양한 distance function들(l1,l2,hamming distance, etc)이 있기때문에 다양한 방법으로 실험을 해야합니다.
이러한 다양한 factor들을 hyperparamter라고 합니다.
또한, 최적의 hyperparamter를 찾는 과정을 hyperparameter tuning이라고 합니다.
어떠한 데이터를 가지고있을 때, 학습을 하기위해서 training과 test로 데이터를 나눕니다.
test데이터는 테스트하기전까지 절대 건드리면 안되는 것입니다. 이유는 분류기를 만들때의 궁극적인 목표가 한번도 보지 않은 데이터를 얼마나 정확하게 분류할 수 있는가 이기 때문입니다.
학습이 잘 되고 있는지 확인하기 위해서 train 데이터의 일부를 validation 데이터로 사용합니다.
이 validation데이터로 학습이 잘 되는지 검증을 하는 것입니다.

이보다 더 발전된 방법이 위의 그림과 같은 cross-validation방법입니다.
train데이터를 k개의 그룹으로 나누어서 1그룹을 validation 데이터로, 나머지는 train데이터로 사용하여 학습을 합니다.
이런 과정을 k번 반복해서 hypterparameter를 튜닝함으로써 분류기를 더욱 일반화시킬 수 있습니다.
한계점
k-nearest neighbor 는 영상 분류기로 사용하기에는 다양한 한계점이 있습니다.
처음 본문에서 언급했던 영상을 분류하는데 chanllenging한 점이 모두 해당되는데, 픽셀간 거리로 판단하기 때문에 약간의 변형만 일어나도 정확한 분류를 할 수 없게 됩니다.
또한, 영상의 차원이 높아질 수록 확인해야하는 픽셀수가 기하급수적으로 늘어나는 “차원의 저주(Curse of dimensionality)”가 일어나게 됩니다.
영상 분류를 할 때 쓰이지는 않지만, 다른 부분에 쓰이는 경우도 간혹 있습니다.